- Michele Vinci
- Informazione Tecnica
- 0 commenti
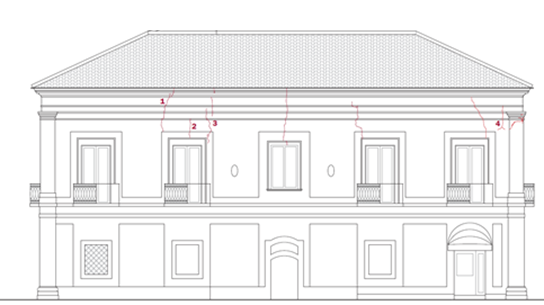
In questa prima parte delle quattro che seguiranno sul nostro Magazine, l'ingegnere Michele Vinci e l'ingegnere Alessandra Caminiti si concentrano sugli edifici in muratura e ci illustrano in maniera sintetica il calcolo di un edificio in muratura dove viene specificato come definire l'indicatore di rischio sismico.
Vi ricordiamo che per approfondire la materia potete sfogliare l'anteprima gratuita di "Metodi di calcolo e tecniche di consolidamento per edifici in muratura" nella sua terza edizione. Buona lettura!
1 - Descrizione generale del manufatto

- Figura 1.a – Stato dell’edificio nei primi anni del secolo scorso
La destinazione d’uso è di civile abitazione. L’obiettivo della committenza è quello di mettere in sicurezza l’edificio nei confronti dei carichi verticali e di quelle sismiche.
Il manufatto è di tipo storico monumentale, per cui soggetto al parere della sovrintendenza.

L’edificio è realizzato con struttura portante in muratura (pietrame disordinato) su due livelli. Gli orizzontamenti del primo livello sono costituitI da volte a botte. Il tetto è costituito da travi in legno e arcarecci, ma date le pessime condizioni e l’abbandono, è richiesto un intervento strutturale.
Le coordinate geografiche del manufatto sono:
-
Longitudine: 16.1788
-
Latitudine: 38.1484
2 – Normativa di riferimento
L'edificio è stato calcolato nel rispetto delle seguenti normative:
D.M. 17/01/2018 - Norma tecniche per le costruzioni
Circolare 7/2019 - Istruzioni per l'applicazione delle norme tecniche per le costruzioni
Circolare 26/2010 - Linee Guida per la valutazione e riduzione del rischio sismico del patrimonio culturale allineate alle nuove Norme tecniche per le costruzioni (d.m. 14 gennaio 2008).
CNR: DT200 R1/2013 - Istruzioni per
3 – Descrizione dell’edificio
La struttura portante dell’edificio è in muratura ordinaria. La tipologia di muratura per gli elementi verticali può essere assimilata a quella che nella Circolare 7/2019 è definita come Pietrame disordinata (vedi figura 2.a). Gli orizzontamenti del primo livello sono delle volte a botte realizzate con mattoni pieni. Per queste ultime il materiale può essere assimilato a quello che nella suddetta Circolare viene definito come Mattoni pieni e malta di calce. Il tetto è costituito da capriate, travi portanti ed arcarecci in legno. Le strutture del tetto sono notevolmente degradate che richiedono necessariamente interventi (vedi figura 2.b).

- Figura 2.a – Tipologia di muratura


- Figura 2.b – Stato di fatto del tetto
Diverse pareti (soprattutto sulle facciate esterne dell’edificio) presentano lesioni importanti. Quanto detto è visibile nelle foto e dagli elaborati (vedi figure 3). Le lesioni possono essere attribuite alle scarse caratteristiche meccaniche della muratura, all’assenza di elementi resistenti a trazione in corrispondenza degli orizzontamenti (cordoli, tiranti, ecc.) ed alla presenza di elementi spingenti (volte a botte e travi del tetto). Non sono stati riscontrati cedimenti del terreno di fondazione (terreno di buona qualità).

- Figura 3.a – Lesioni sulla facciata
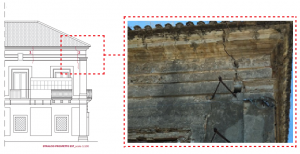
- Figura 3.b – Lesioni al cantonale
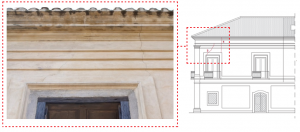
- Figura 3.c – Lesioni su finestra
Le fondazioni sono in muratura di mattoni pieni e non presentano stati di cedimenti.
3.1 – Elaborati architettonici
Di seguito si riportano le piante di ogni piano della costruzione. A titolo dimostrativo si riporta anche un prospetto.
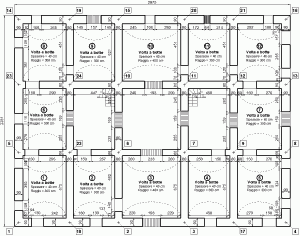
- Figura 4.a – Pianta primo piano fuori terra
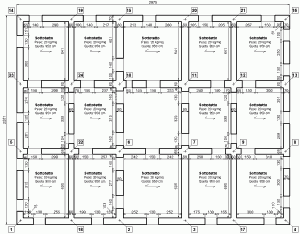
- Figura 4.b – Pianta secondo piano fuori terra
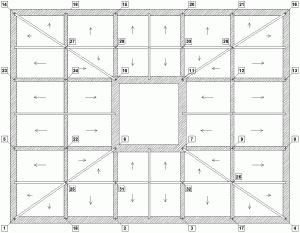
- Figura 4.c – Pianta copertura
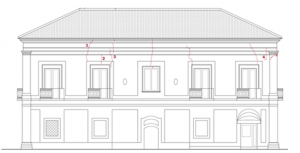
- Figura 4.d – Prospetto
4 – Valutazione della classe di rischio della struttura
Secondo le indicazioni di normativa, l’edificio deve essere verificato secondo le combinazioni fondamentali e quelle sismiche. Le verifiche secondo le combinazioni fondamentali devono dare esito positivo. Secondo il punto 8.3 del D.M. 17/01/2018, se le verifiche fondamentali non sono soddisfatte, l’edificio deve essere declassato. Per poter parlare di resistenza sismica di una struttura, è necessario che siano soddisfatte le verifiche relative alle combinazioni fondamentali.
La resistenza sismica di un edificio si valuta attraverso l’indicatore di rischio (zE,SL). Il suddetto indicatore può assumere un valore maggiore o uguale a zero. Se assume il valore 0, la struttura non è in grado di resistere ad alcuna azione sismica. Se l’edificio non è capace di soddisfare le verifiche statiche, non ha la capacità di resistere ad azioni sismiche di qualsiasi entità. Se l’indicatore di rischio assume un valore non minore di 1, l’edificio soddisfa pienamente le richieste di normativa ai fini della resistenza nei confronti delle azioni sismiche (struttura adeguata).
Se l’indicatore di rischio è compreso tra 0 ed 1, la struttura ha una certa resistenza nei confronti delle azioni sismiche, ma non sufficiente a soddisfare le esigenze di normativa. In particolare, se l’indicatore di rischio è più vicino a 0, la struttura ha limitate risorse di resistenza nei confronti delle azioni sismiche. Se vicino ad
L’edificio deve essere sottoposto alle verifiche statiche previste dal capitolo 4 del D.M. 17/01/2018 ed alle verifiche sismiche previste dal capitolo 7 del medesimo decreto. Trattandosi di un edificio in muratura, è opportuno effettuare le verifiche secondo analisi di tipo globale (per esempio, analisi statica non lineare – pushover) e secondo analisi di tipo locale (per esempio, analisi dei meccanismi locali). La sicurezza della struttura si ottiene dalla verifica che fornisce l’indicatore di valore minore.
4.1 – Criticità della struttura
L’edificio oggetto di studio presenta diverse criticità. Come accennato sopra, le strutture portanti del tetto sono realizzate con capriate in legno ed arcarecci. Questi ultimi poggiano sulle capriate, su travi portanti e sui timpani delle pareti (vedi figure 2). Come si può vedere dalle figure, gli elementi strutturali sono particolarmente degradati.
Molte pareti, in particolare le facciate esterne, presentano un quadro fessurativo importante (vedi figure 3). La motivazione delle fessure è da attribuire alla scarsa qualità della muratura in termini di resistenza ed alla presenza di alcuni elementi spingenti in corrispondenza del tetto. Non sono da attribuire a cedimenti di fondazione in quanto si presentano in ottimo stato.
Anche le volte a botte presentano alcune criticità. In particolare, quelle che spingono sui muri esterni, presentano lesioni all’intradosso in corrispondenza della mezzeria. Le lesioni possono essere attribuite alla scarsa capacità dei muri su cui poggiano a contrastare le spinte statiche orizzontali generate dalle volte, provocando il conseguente rilassamento delle stesse volte.
4.2 – Valutazione dell’azione sismica
L’azione sismica con la quale verificare la struttura viene valutata attraverso il metodo semplificato previsto dalla normativa. Con tale metodo è sufficiente conoscere le coordinate geografiche del sito, il suolo di fondazione e la categoria topografica (dati generalmente ricavabili dalla relazione geologica). Per la struttura oggetto di studio, dalla relazione geologica redatta da geologo qualificato si riscontra una categoria di sottosuolo B e la categoria topografica T1. Essendo note anche le coordinate del sito (vedi sopra), è possibile definire l’azione sismica. Nelle successive tabelle si riportano i parametri che definiscono gli spettri per tutti gli stati limite (SLC, SLV, SLD ed SLO).
|
|
ag |
F0 |
Tc* [s] |
S |
TB [s] |
TC [s] |
TD [s] |
Se,max [cm/s2] |
|
SLC |
0.258 |
2.414 |
0.388 |
1.151 |
0.172 |
0.516 |
2.632 |
702.9 |
|
SLV |
0.193 |
2.398 |
0.369 |
1.200 |
0.165 |
0.495 |
2.372 |
544.6 |
|
SLD |
0.065 |
2.348 |
0.303 |
1.200 |
0.141 |
0.423 |
1.860 |
179.6 |
|
SLO |
0.050 |
2.348 |
0.278 |
1.200 |
0.132 |
0.395 |
1.800 |
138.1 |
Tabella 1 – Parametri che definiscono l’azione sismica secondo il metodo semplificato proposto dal punto 3.2.3 del D.M. 17/01/2018 per tutti gli stati limite
4.3 – Valutazione dei parametri meccanici dei materiali
Il calcolo della struttura richiede la conoscenza dei parametri meccanici dei materiali di cui è costituita. La valutazione dei suddetti parametri prevede una diagnostica sulla struttura più o meno approfondita. La gestione dei parametri meccanici della muratura è regolata dal punto C8.5.3.1 della Circolare 7/2019 secondo cui è possibile raggiungere tre livelli di conoscenza (LC1, LC2 ed LC3) in funzione delle indagini effettuate (distruttive e non distruttive). Per la muratura, è possibile limitare le indagini solamente a quelle non distruttive. Tale limitazione è possibile solo per il livello di conoscenza LC1. Per tale livello di conoscenza i parametri meccanici si definiscono esclusivamente dalla tabella C8.5.I della Circolare, assumendo i valori minimi per quanto riguarda le resistenze (fm, t0 e fv0) ed i valori medi per quanto riguarda i moduli elastici (E e G).
I parametri di resistenza devono essere divisi per il fattore di confidenza (FC) che per il livello di conoscenza LC1 vale 1.35 ed il coefficiente di sicurezza (gm) che per le verifiche statiche si assume pari a 2.5 e per quelle sismiche si assume pari a 2.0. Nella tabella 2 si riportano i parametri meccanici per i materiali interessati dalla struttura oggetto di studio (pietrame disordinata per gli elementi strutturali verticali e mattoni pieni e malta di calce per gli archi e le volte).
|
Tipologia di muratura |
fm [daN/cm2] |
t0 [daN/cm2] |
fv0 [daN/cm2] |
E [daN/cm2] |
G [daN/cm2] |
w [daN/m3] |
|
min - max |
min - max |
min - max |
min - max |
min - max |
||
|
Muratura in pietrame disordinata (ciottoli, pietre erratiche e irregolari) |
10.0 20.0 |
0.18 0.32 |
- - |
6900 10500 |
2300 3500 |
1900 |
|
Muratura in mattoni pieni e malta di calce (***) |
26.0 43.0 |
0.50 1.30 |
1.30 2.70 |
12000 18000 |
4000 6000 |
1800 |
Tabella 2 – Parametri meccanici forniti dalla tabella C8.5.I della Circolare 7/2019
Nella tabella 3 si riportano i parametri meccanici tenendo conto del fattore di confidenza (FC) e del coefficiente di sicurezza (gm).
|
Tipologia di muratura |
gm |
FC |
fd [daN/cm2] |
t0d [daN/cm2] |
fvd0 [daN/cm2] |
E [daN/cm2] |
G [daN/cm2] |
w [daN/m3] |
|
Muratura in pietrame disordinata (ciottoli, pietre erratiche e irregolari) |
2.5 |
1.35 |
2.96 |
0.053 |
0.053 |
8700 |
2900 |
1900 |
|
Muratura in mattoni pieni e malta di calce (***) |
2.5 |
1.35 |
7.70 |
0.148 |
0.32 |
15000 |
5000 |
1800 |
Tabella 3.a – Parametri meccanici di calcolo per le verifiche ai carichi statici
|
Tipologia di muratura |
gm |
FC |
fd [daN/cm2] |
t0d [daN/cm2] |
fvd0 [daN/cm2] |
E [daN/cm2] |
G [daN/cm2] |
w [daN/m3] |
|
Muratura in pietrame disordinata (ciottoli, pietre erratiche e irregolari) |
2.0 |
1.35 |
3.71 |
0.066 |
0.066 |
8700 |
2900 |
1900 |
|
Muratura in mattoni pieni e malta di calce (***) |
2.0 |
1.35 |
9.63 |
0.185 |
0.40 |
15000 |
5000 |
1800 |
Tabella 3.b – Parametri meccanici di calcolo per le verifiche sismiche
4.4 – Analisi della struttura
Prima di affrontare il calcolo dell’edificio oggetto di studio è doveroso fare alcune considerazioni sugli edifici in muratura. Per grosse linee, i suddetti edifici possono essere catalogati in tre categorie:
1) edifici di classe I: sia le pareti verticali che gli orizzontamenti sono realizzati in muratura. È il caso di costruzioni più antiche dove gli orizzontamenti sono realizzati con archi e volte. Questa tipologia di edifici è spesso soggetta alla perdita di equilibrio di alcuni elementi (soprattutto sotto gli effetti dinamici) che ne generano il conseguente crollo;
2) edifici di classe II: gli elementi verticali sono realizzati in muratura mentre quelli orizzontali hanno la caratteristica di essere scarsamente rigidi nel proprio piano (generalmente realizzati con travi in legno e tavolato o con putrelle metalliche e tavelloni). Questi edifici hanno il tipico comportamento detto “a carciofo” (gli elementi verticali non sono collegati tra di loro dai solai per cui, sotto gli effetti dinamici, subiscono spostamenti tra di loro indipendenti);
3) edifici di classe III: gli elementi verticali sono realizzati in muratura e quelli orizzontali hanno la caratteristica di poter essere considerati rigidi nel proprio piano. Questi edifici sono generalmente di più recente realizzazione ed i solai sono di tipo latero-cementizio delimitati da cordoli in cemento armato. Il comportamento di questi edifici sotto gli effetti dinamici è quello tipico “scatolare”. A differenza delle prime due tipologie di edifici, i solai contribuiscono alla ripartizione delle azioni sismiche sugli elementi verticali.
Nel nostro caso, sia gli elementi verticali (pareti in muratura) che gli orizzontamenti (archi e volte) sono in muratura e non sono presenti elementi resistenti a trazione in corrispondenza degli orizzontamenti (cordoli, tiranti, ecc.). Tenendo conto delle tre categorie di edifici sopra riportate, l’edificio oggetto di studio può essere collocato nella categoria classe I. Quindi, ci si aspetta una risposta strutturale più carente per le verifiche di tipo locale (meccanismi locali) rispetto a quelle di tipo globale (pushover).
Come accennato sopra, l’edificio deve essere analizzato sia secondo le verifiche statiche che secondo quelle sismiche.
Infine, vista la complessità della struttura, si fa utilizzo di software di calcolo dedicati (vedi software utilizzati). Nella figura 5 si riporta una vista 3D del modello strutturale.
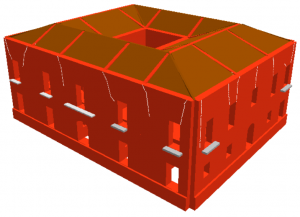
- Figura 5 – Modello strutturale senza interventi (software VEMNL)
4.4.1 – Verifiche a carichi statici
Le verifiche in assenza di azione sismica sono riportate nel capitolo 4 del D.M. 17/01/2018. Si tiene conto soltanto dei carichi verticali e di eventuali carichi statici (neve, vento, terreno, ecc.). Le combinazioni di carico sono quelle fondamentali (SLU). Si riporta di seguito la verifica a carichi laterali e consiste nel confrontare lo sforzo normale sollecitante (NSd) che si ottiene dall’analisi della struttura con quello resistente (NRd) che dipende dalle caratteristiche meccaniche del materiale (resistenza a compressione della muratura fd), dalla snellezza della parete (l), dall’eccentricità dei carichi (m) e dall’area della sezione trasversale dell’elemento strutturale in muratura (A). Affinché l’esito della verifica sia soddisfatto deve essere verificata la seguente:
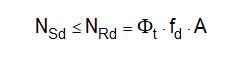 (1)
(1)
Il coefficiente Ft si ottiene dalla tabella 4 (fornita dal D.M. 17/01/2018), in funzione della snellezza della parete (l) e del coefficiente di eccentricità (m):
|
Snellezza [l] |
Coefficiente di eccentricità m = 6 × e / t |
||||
|
0.0 |
0.5 |
1.0 |
1.5 |
2.0 |
|
|
0 |
1.00 |
0.74 |
0.59 |
0.44 |
0.33 |
|
5 |
0.97 |
0.71 |
0.55 |
0.39 |
0.27 |
|
10 |
0.86 |
0.61 |
0.45 |
0.27 |
0.15 |
|
15 |
0.69 |
0.48 |
0.32 |
0.17 |
--- |
|
20 |
0.53 |
0.36 |
0.23 |
--- |
--- |
Tabella 4 – Valori di Ft in funzione della snellezza della parete e dell’eccentricità dei carichi
Come si può vedere dai dati riportati in tabella 4, il coefficiente Ft diminuisce (e quindi lo sforzo normale resistente NRd) all’aumentare della snellezza e dell’eccentricità dei carichi. A titolo di esempio si riporta il calcolo in testa del maschio murario compreso tra i fili fissi 7-9 (parete evidenziata in rosso nella figura 7). Poiché il calcolo viene sviluppato manualmente, si effettuano alcune semplificazioni. Sulla parete oggetto di verifica grava il peso della parete al piano superiore ed una rampa di scale.
|
Tipologia di carico |
Carico caratteristico [daN] |
Coefficiente di combinazione |
Carico di calcolo [daN] |
|
Peso proprio della parete al piano superiore |
20450 |
1.3 |
26585 |
|
Peso pianerottolo scala |
3375 |
1.3 |
4387 |
|
Carico di esercizio scala |
2700 |
1.5 |
4050 |
|
Sforzo normale sollecitante (NSd) |
- |
- |
35022 |
Tabella 5 – Carichi sulla testa del muro e valutazione dello sforzo normale sollecitante (NSd)
Essendo il maschio murario lungo 250 cm ed avendo uno spessore di 66 cm (vedi figura 7), si ottiene l’area della sezione trasversale pari a A = 16500 cm2. Per valutare il coefficiente Ft che compare nella formula (1), occorre definire la snellezza (l) ed il coefficiente di eccentricità (m). Ipotizzando il maschio murario non irrigidito dalla presenza dei muri ortogonali, si ottiene il valore della snellezza riportata nella (2):
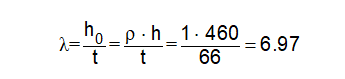 (2)
(2)
Per valutare il coefficiente di eccentricità (m), occorre valutare il punto di applicazione dei carichi verticali sulla testa della parete. Considerando il carico della parete al piano superiore in asse al muro oggetto di studio e la risultante del balcone applicata a 7.5 cm dal bordo della parete (vedi figura 6). Indicando con N1 la forza dovuta alla parete superiore e con N2 quella del balcone ed indicando con d1 la distanza di N1 dal lembo esterno della parete e con d2 quella del balcone, si ottiene l’eccentricità (es) dovuta ai carichi:
![]()
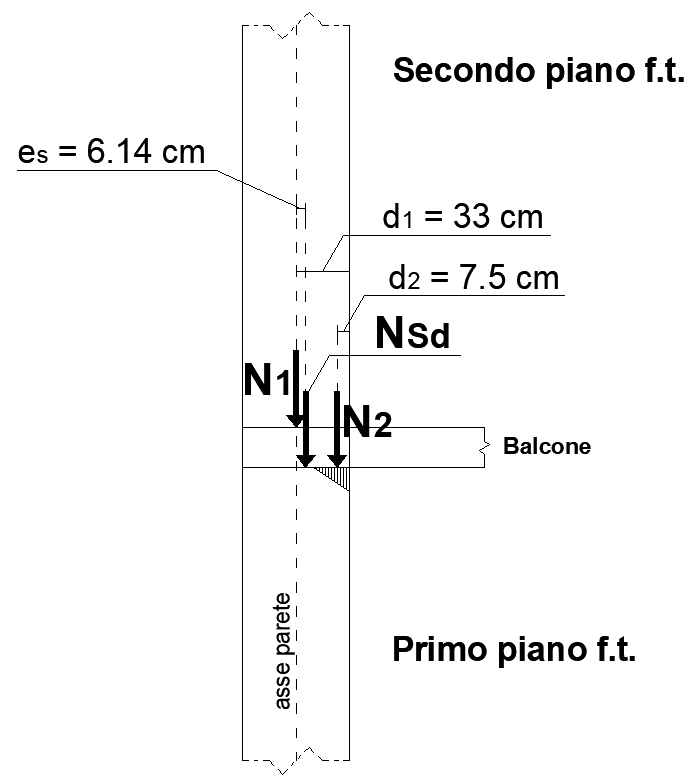
- Figura 6 – Valutazione dell’eccentricità dei carichi
Oltre all’eccentricità data dalla (3), occorre considerare quella dovuta ai difetti di costruzione data dalla seguente:
![]()
In definitiva, l’eccentricità totale vale:
![]()
Nota l’eccentricità, è possibile valutare il coefficiente (m):

Nelle tabelle 6 si riportano i risultati di tutti i maschi murari di cui è costituita la struttura. La verifica viene effettuata sia nella sezione di testa che in quella di mezzeria. Per evitare inutili lungaggini, si riportano soltanto i risultati degli elementi per cui l’esito della verifica è negativo.
|
Verifica carichi verticali nella sezione di mezzeria |
|||||||||||
|
Fili |
Piano |
Maschio |
NSd [daN] |
l |
m |
F |
A [cm²] |
fd [daN/cm²] |
NRd [daN] |
S |
Esito |
|
6, 7 |
1 |
1 |
35578 |
6.97 |
0.10 |
0.87 |
13200 |
2.96 |
33993 |
0.96 |
NV |
|
6, 7 |
1 |
2 |
35578 |
6.97 |
0.10 |
0.87 |
13200 |
2.96 |
33993 |
0.96 |
NV |
|
6, 10 |
1 |
1 |
67172 |
5.75 |
0.21 |
0.85 |
18800 |
2.96 |
47301 |
0.70 |
NV |
|
6, 10 |
1 |
2 |
76140 |
5.75 |
0.20 |
0.85 |
20400 |
2.96 |
51326 |
0.67 |
NV |
|
22, 6 |
1 |
1 |
11644 |
6.97 |
0.26 |
0.80 |
2640 |
2.96 |
6252 |
0.53 |
NV |
|
22, 6 |
1 |
2 |
42449 |
6.97 |
0.24 |
0.80 |
16962 |
2.96 |
40166 |
0.95 |
NV |
|
7, 9 |
1 |
1 |
43482 |
6.97 |
0.30 |
0.77 |
16500 |
2.96 |
37607 |
0.87 |
NV |
|
7, 9 |
1 |
2 |
13907 |
6.97 |
0.31 |
0.77 |
3300 |
2.96 |
7521 |
0.54 |
NV |
|
11, 7 |
1 |
1 |
74053 |
5.75 |
0.15 |
0.87 |
18800 |
2.96 |
48414 |
0.66 |
NV |
|
11, 7 |
1 |
2 |
70658 |
5.75 |
0.16 |
0.87 |
20400 |
2.96 |
52534 |
0.74 |
NV |
|
9, 12 |
1 |
1 |
69392 |
5.75 |
0.20 |
0.85 |
18800 |
2.96 |
47301 |
0.68 |
NV |
|
9, 12 |
1 |
2 |
73622 |
5.75 |
0.20 |
0.85 |
20400 |
2.96 |
51326 |
0.70 |
NV |
|
15, 19 |
1 |
1 |
33164 |
5.11 |
0.43 |
0.74 |
13050 |
2.96 |
28585 |
0.86 |
NV |
|
24, 22 |
1 |
1 |
69865 |
5.75 |
0.20 |
0.85 |
18800 |
2.96 |
47301 |
0.68 |
NV |
|
24, 22 |
1 |
2 |
72718 |
5.75 |
0.21 |
0.85 |
20400 |
2.96 |
51326 |
0.70 |
NV |
Tabella 6.a –Verifica carichi verticali nella sezione di mezzeria
|
|
Verifica carichi verticali nella sezione di testa |
||||||||||||
|
Fili fissi |
Piano |
Maschio |
NSd [daN] |
l |
m |
F |
A [cm²] |
fd [daN/cm²] |
NRd [daN] |
S |
Esito |
|
|
|
6, 10 |
1 |
1 |
56492 |
5.75 |
0.42 |
0.74 |
18800 |
2.96 |
41180 |
0.73 |
NV |
|
|
|
6, 10 |
1 |
2 |
64550 |
5.75 |
0.40 |
0.75 |
20400 |
2.96 |
45288 |
0.70 |
NV |
|
|
|
22, 6 |
1 |
1 |
10144 |
6.97 |
0.51 |
0.67 |
2640 |
2.96 |
5236 |
0.51 |
NV |
|
|
|
7, 9 |
1 |
1 |
35022 |
6.97 |
0.77 |
0.57 |
16500 |
2.96 |
28816 |
0.82 |
NV |
|
|
|
7, 9 |
1 |
2 |
12032 |
6.97 |
0.63 |
0.63 |
3300 |
2.96 |
6154 |
0.51 |
NV |
|
|
|
11, 7 |
1 |
1 |
63373 |
5.75 |
0.31 |
0.79 |
18800 |
2.96 |
43962 |
0.69 |
NV |
|
|
|
11, 7 |
1 |
2 |
59069 |
5.75 |
0.33 |
0.78 |
20400 |
2.96 |
47100 |
0.80 |
NV |
|
|
|
9, 12 |
1 |
1 |
58712 |
5.75 |
0.41 |
0.74 |
18800 |
2.96 |
41180 |
0.71 |
NV |
|
|
|
9, 12 |
1 |
2 |
62033 |
5.75 |
0.41 |
0.74 |
20400 |
2.96 |
44684 |
0.72 |
NV |
|
|
|
15, 19 |
1 |
1 |
25750 |
5.11 |
0.87 |
0.59 |
13050 |
2.96 |
22791 |
0.89 |
NV |
|
|
|
24, 22 |
1 |
1 |
59185 |
5.75 |
0.40 |
0.74 |
18800 |
2.96 |
41180 |
0.70 |
NV |
|
|
|
24, 22 |
1 |
2 |
61129 |
5.75 |
0.41 |
0.74 |
20400 |
2.96 |
44684 |
0.73 |
NV |
|
|
Tabella 6.b –Verifica carichi verticali nella sezione di testa
Nella figura 7 vengono visualizzati graficamente gli elementi per cui l’esito della verifica è negativo.
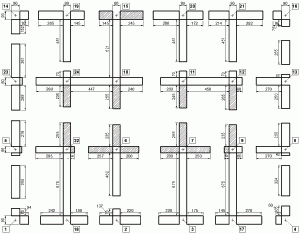
- Figura 7 – Elementi che non soddisfano la verifica a carichi laterali (tratteggiati in figura)
Oltre alle verifiche degli elementi verticali, occorre verificare ai carichi statici anche gli elementi orizzontali (volte a botte). Nelle figura 8.a si riporta la curva delle pressioni di alcune delle volte di cui è costituita la struttura (volte indicate con i numeri 1, 2, 3, 4 e 5 di figura 9). Come si può vedere, le volte 1 e 5 presentano delle parzializzazioni importanti all’intradosso in mezzeria. Le volte 2, 3 e 4 vengono bilanciate da quelle adiacenti per cui presentano parzializzazioni minori, mentre le volte 1 e 5 devono fare affidamento soltanto sulle pareti su cui poggiano. Per effetto delle spinte statiche orizzontali, i piedritti tendono a ruotare, generando il conseguente rilassamento delle volte.

- Figura 8.a – Curva delle pressioni delle volte in assenza di interventi
Nella figura 8.b si riporta l’esito della verifica a pressoflessione (le parti in rosso sono quelle non verificate).

- Nella figura 8.b si riporta l’esito della verifica a pressoflessione (le parti in rosso sono quelle non verificate).
Nella figura 9 si riportano tutte le volte a botte della struttura per cui l’esito della verifica è negativo.
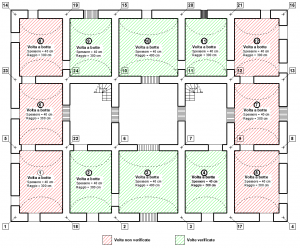
- Figura 9 – Volte con esito negativo delle verifiche (tratteggiate in rosso)
Dalla soluzione del sistema voltato si ottengono le spinte orizzontali che gravano sulle pareti. Nella figura 10 si riporta il valore della spinta statica generata dalla volta contrassegnata dal numero 5 che grava sulla parete 8-4 (parete evidenziata in rosso in figura 12). La spinta viene presa in considerazione nel calcolo del meccanismo della suddetta parete.
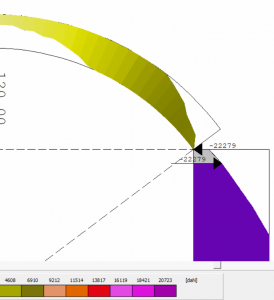
- Figura 10 – Spinta statica generata dalla volta a botte indicata con il numero 5 in figura 7
4.4.2 – Analisi dei meccanismi locali
Si effettua la verifica secondo l’analisi cinematica lineare riportata nel punto C8.7.1.2 della Circolare 7/2019. La verifica viene effettuata a ribaltamento semplice e flessione verticale per tutte le pareti di cui è costituita la struttura, considerando diverse posizioni delle cerniere cinematiche. Si assumono i risultati relativi alla posizione di cerniera che fornisce gli indicatori di rischio più bassi. Come fatto per le verifiche in assenza di sisma, anche in questo caso si effettua manualmente il calcolo di una sola parete e si riportano in sintesi i risultati di tutte le altre pareti per cui l’esito della verifica è negativo. Si effettua la verifica per lo stato limite di salvaguardia della vita (SLV). Si sviluppa manualmente il calcolo del meccanismo a ribaltamento semplice della parete 8-4 (parete evidenziata in rosso in figura 12). Nella figura 11 e nella tabella 6 si riportano i carichi che gravano sulla parete e le distanze dalla cerniera cinematica C. Sul meccanismo gravano le forze peso stabilizzanti delle pareti (W1 e W2), le forze stabilizzanti dovute al balcone ed al tetto (S1 e S2), la forza stabilizzante verticale dovuta alla volta (Sv), la forza stabilizzante dovuta alla parete ortogonale al primo piano f.t. (M1 - si considera solo la parete 9-8. La forza stabilizzante della parete ortogonale 4-17 si ritiene trascurabile per via delle modestissime dimensioni del maschio murario), la forza destabilizzante dovuta alla spinta orizzontale della volta (So), la forza destabilizzante dovuta alla spinta orizzontale dei travetti del tetto (So2) e le forze destabilizzanti inerziali (a0∙W1, a0∙W2, a0∙S1, a0∙S2 e a0∙Sv).
|
Forze agenti sulla catena cinematica |
X [cm]</p |

Commenti (0)
Aggiungi nuovo commento